the backpropagation algorithm

Published: December 14, 2018 by

• Categories:
• note 2

• Tags:
• algorithm 1
• neural-network 1

intro

이번 글에서는 BP(Backpropagation) Algorithm에 대해 정리해보도록 하겠습니다. 이글은 특히 B.P. 의 수식을한번 깔끔하게 정리해보는데 그 목표를 두고 있습니다. 이 포스트를 작성하면서 Cousera의 Andrew Ng 교수님의 Machine Learning 강좌를 많이 참고하였음을 먼저 밝힙니다. 아래 등장하는 Notation들 역시 해당 강의에서 사용하는 Notation을 사용하였습니다. 글은 간단한 소개로 시작하여, Notation, Definition을 이어 설명하고, 메인이 되는 B.P. Algorithm 을 서술하고 이를 증명하는 순서로 작성하였습니다.

BP란 머신러닝 모형들중 Neural Network에서 등장하는 알고리즘입니다. 조금 더 구체적으로, 보통 머신러닝 모형은 Cost Function을 Minimize하는 방식으로 모형을 데이터에 적합을 시키는데 이때 Cost Function의 Gradient를 계산하게 됩니다. 여기서 Neural Network는 그 특성상 구조가 복잡하여 해당하는 Gradient를 계산하는데 많은 계산이 필요하여 효율적인 계산이 필요하게 되고 이를 구현한것이 바로 Backpropagation Algorithm이 되겠습니다. 붙여진 이름은 알고리즘 내의 특정값들이 계산되는 방향이 뒤에서 앞쪽으로(Back) 흘러가기때문에 그렇습니다.

notation, convention

Newral Network의 BP를 설명하기 위해서는 아래와같은 기호들이 필요합니다.
충분히 기호가 많기 때문에 식을 전개할때, 특정 example을 지칭하는 $(i)$ 는 생략하도록 하였습니다.

• $n$ : number of features.
• $m$ : number of examples.
• $L$ : total number of layers in the network.
• $S_l$ : number of units in layer $l$ (not containing bias unit).
• $\theta^{(l)}_{ij}$ : parameter from $j$-th unit of $l$-th layer to $i$-th unit of $(l+1)$-th layer.
• $z^{(l)(i)}_x$ $(= z^{(l)}_x)$ : $x$-th unit of $l$-th layer for the $i$-th example.
• $a^{(l)(i)}_x$ $(= a^{(l)}_x)$ : activation of $z^{(l)(i)}_x$.
• $\delta^{(l)(i)}_x$ $(= \delta^{(l)}_x)$.
• $h_{\theta}(x)$ : the Hypothesis function of data x with the parameter $\theta$.
• $J(\theta)$ : the Cost function.

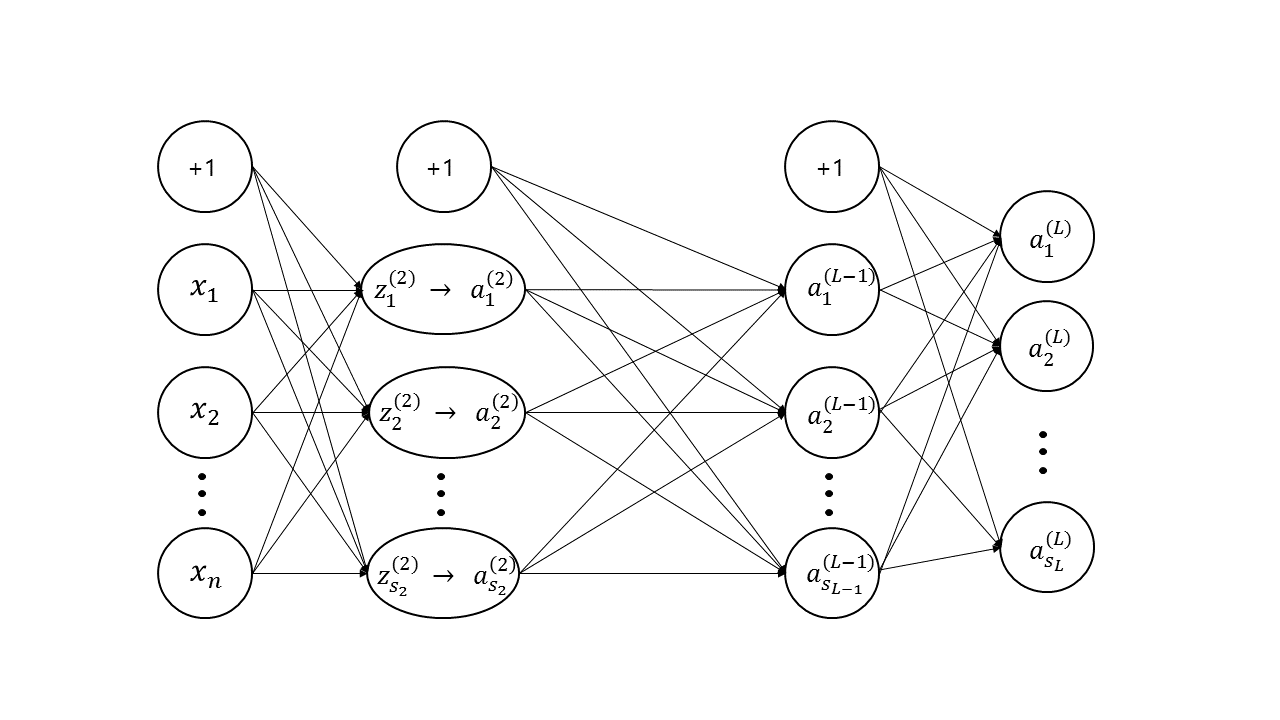
Definition

위에서 언급된 여러 기호들에 대하여 아래와 같이 정의함으로써 Neural Network Classifier를 설계하도록 합니다.
여기서, activation function으로는 sigmoid function만을 고려하였습니다.

\[\begin{aligned} z^{(l)}_x &= \theta^{(l-1)}_{x0}a^{(l-1)}_0 + \theta^{(l-1)}_{x1}a^{(l-1)}_1 + \cdots + \theta^{(l-1)}_{xS_{L-1}}a^{(l-1)}_{S_{l-1}}.\\ a^{(l)}_x &= g(z_x^{(l)}). \\ g(z) &= \frac{1}{1+e^{-z}}. \\ h_{\theta}(x) &= \Big(g(z_1^{(L)}),g(z_2^{(L)}),\cdots,g(z_{S_L}^{(L)})\Big). \\ (h_{\theta}(x))_t &= g(z_t^{(L)}). \\ J(\theta) &= - \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \log(h_{\theta}(x)_t) + (1-y_t)\log(1-h_{\theta}(x)_t) \Big]. \\ y^{(i)}&= y \\ &= S_L \times 1 \text{ vector of i-th example that represent class which belongs to}. \\ y_t &= \begin{cases} 1 \text{ if i-th example is belongs to t-th class}\\ 0 \text{ otherwise.} \end{cases} \end{aligned}\]

The algorithm

The BackPropagation Algorithm : 간단한 Fully connected neural network는 아래와같이  gradient를 효율적으로 계산해 낼 수 있다. 

\[\frac{\partial}{\partial \theta^{(l)}_{kj}} J(\theta) = \frac{1}{m} \sum^m_{i=1}\Big[a^{(l)(i)}_j \delta^{(l+1)(i)}_k \Big] \text{,}\]

where

\[\begin{aligned} \delta^{(L)}_k &= a^{(L)}_k - y_k, \quad k=1 \cdots S_L ,\\ \delta^{(l)}_k &= g'(z^{(l)}_k) \sum^{S_{l+1}}_{j=1} \Big[ \delta^{(l+1)}_j \theta^{(l)}_{jk} \Big], \quad k = 1 \cdots S_l, l = 1 \cdots L-1 \end{aligned}\]

Backpropagation Algorithm을 증명하기위해 두개의 Lemma를 활용하였습니다.
먼저 정리와 Lemma를 서술하였고, 이후 증명을 작성하였습니다.

• Lemma 1

\[\frac{\partial}{\partial \theta^{(l)}_{kj}} J(\theta) = \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ \frac{\partial z_t^{(L)}}{\partial \theta^{(l)}_{kj}} \delta_t^{(L)} \Big] ,\quad l = 1,\cdots,L-1\]

• Lemma 2

\[\sum_{t=1}^{S_L} \frac{\partial z_t^{(L)}}{\partial a^{(l)}_{x}} \delta^{(L)}_t = \theta_{1x}^{(l)}\delta_1^{(l+1)}+\theta_{2x}^{(l)}\delta_2^{(l+1)} + \cdots + \theta_{S_{l+1}x}^{(l)}\delta_{S_{l+1}}^{(l+1)},\quad l = 1,\cdots,L-1\]

증명

Proof of Theorem(Backpropagation Algorithm)

$l = L-1$ 일때,

\[\begin{aligned} \frac{\partial}{\partial \theta^{(L-1)}_{kj}} J(\theta) &= \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ \frac{\partial z_t^{(L)}}{\partial \theta^{(L-1)}_{kj}} \delta_t^{(L)} \Big], \text{ by Lemma 1} \\ &= \frac{1}{m} \sum^m_{i=1} \Big[a_j^{(L-1)} \delta_k^{(L)} \Big] \end{aligned}\]

$l < L-1$ 일때,

\[\begin{aligned} \frac{\partial}{\partial \theta^{(l)}_{kj}} J(\theta) &= \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ \frac{\partial z_t^{(L)}}{\partial \theta^{(l)}_{kj}} \delta_t^{(L)} \Big], \text{ by Lemma 1} \\ &= \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ \frac{\partial a_k^{(l+1)}}{\partial \theta^{(l)}_{kj}} \frac{\partial z_t^{(L)}}{\partial a_k^{(l+1)}} \delta_t^{(L)} \Big], \text{ by Chain rule} \\ &= \frac{1}{m} \sum^m_{i=1}\frac{\partial a_k^{(l+1)}}{\partial \theta^{(l)}_{kj}} \Big[\sum^{S_L}_{t=1}\Big[ \frac{\partial z_t^{(L)}}{\partial a_k^{(l+1)}} \delta_t^{(L)} \Big]\Big] \\ &= \frac{1}{m} \sum^m_{i=1}\frac{\partial a_k^{(l+1)}}{\partial \theta^{(l)}_{kj}} \Big[\theta_{1k}^{(l+1)}\delta_1^{(l+2)}+\theta_{2k}^{(l+1)}\delta_2^{(l+2)} + \cdots + \theta_{S_{l+2}k}^{(l+1)}\delta_{S_{l+2}}^{(l+2)} \Big], \text{ by Lemma 2} \\ &= \frac{1}{m} \sum^m_{i=1} a_j^{(l)}g'(z^{(l+1)}_k) \Big[\theta_{1k}^{(l+1)}\delta_1^{(l+2)}+\theta_{2k}^{(l+1)}\delta_2^{(l+2)} + \cdots + \theta_{S_{l+2}k}^{(l+1)}\delta_{S_{l+2}}^{(l+2)} \Big] \\ &= \frac{1}{m} \sum^m_{i=1} \Big[a_j^{(l)} \delta_k^{(l+1)} \Big] , \text{ by Definition of delta} \end{aligned}\]

• Proof of Lemma 1

$J(θ)$의 정의로부터 계산을 해 나가면 아래와 같이 된다.

\[\begin{aligned} J(\theta) &= - \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \log(h_{\theta}(x)_t) + (1-y_t)\log(1-h_{\theta}(x)_t) \Big] \\ &=- \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \log( \frac{1}{1+e^{-z_t^{(L)}}} ) + (1-y_t)\log(1-\frac{1}{1+e^{-z_t^{(L)}}}) \Big] \\ &=- \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \log( \frac{1}{1+e^{-z_t^{(L)}}} ) + (1-y_t)\log(\frac{e^{-z_t^{(L)}}}{1+e^{-z_t^{(L)}}}) \Big] \\ &=- \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ -y_t \log( 1+e^{-z_t^{(L)}} ) + (1-y_t) (-z_t^{(L)} - \log(1+e^{-z_t^{(L)}})) \Big] \\ &=- \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t z_t^{(L)} - z_t^{(L)} - \log(1+e^{-z_t^{(L)}}) \Big] \\ &=- \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t z_t^{(L)} - \log(1+e^{z_t^{(L)}}) \Big] \\ \end{aligned}\]

따라서,

\[\begin{aligned} \frac{\partial}{\partial \theta^{(l)}_{kj}} J(\theta) &= - \frac{\partial}{\partial \theta^{(l)}_{kj}}\frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t z_t^{(L)} - \log(1+e^{z_t^{(L)}}) \Big] \\ &= - \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \frac{\partial}{\partial \theta^{(l)}_{kj}}z_t^{(L)} - \frac{\partial}{\partial \theta^{(l)}_{kj}}\log(1+e^{z_t^{(L)}}) \Big] \\ &= - \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \frac{\partial}{\partial \theta^{(l)}_{kj}}z_t^{(L)} - \frac{\partial}{\partial \theta^{(l)}_{kj}} [z_t^{(L)}] \frac{e^{z_t^{(L)}}}{1+e^{z_t^{(L)}}} \Big] \\ &= - \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \frac{\partial}{\partial \theta^{(l)}_{kj}}z_t^{(L)} - \frac{\partial}{\partial \theta^{(l)}_{kj}} [z_t^{(L)}] \frac{1}{1+e^{-z_t^{(L)}}} \Big] \\ &= - \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ y_t \frac{\partial}{\partial \theta^{(l)}_{kj}}z_t^{(L)} - \frac{\partial}{\partial \theta^{(l)}_{kj}} [z_t^{(L)}] a^{(L)}_t \Big] \\ &= - \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ \frac{\partial}{\partial \theta^{(l)}_{kj}} [z_t^{(L)}](y_t - a_t^{(L)})\Big] \\ &= \frac{1}{m} \sum^m_{i=1}\sum^{S_L}_{t=1}\Big[ \frac{\partial z_t^{(L)}}{\partial \theta^{(l)}_{kj}} \delta_t^{(L)} \Big] \end{aligned}\]

• Proof of Lemma 2

$l$에 대한 귀납법을 이용하여 위 Lemma를 증명하도록 하자.
우리는 간단한 계산을 통해 $l = L-1$ 일때 위 식이 성립함을 확인 할 수 있다.

\[\begin{aligned} \frac{\partial z_t^{(L)}}{\partial a^{(L-1)}_{x}} \delta^{(L)}_t &= \frac{\partial}{\partial a^{(L-1)}_{x}} \Big(z_t^{(L)}\Big) \delta^{(L)}_t\\ &=\frac{\partial}{\partial a^{(L-1)}_{x}} \Big( a_0^{(L-1)}\theta_{t0}^{(L-1)} + a_1^{(L-1)}\theta_{t1}^{(L-1)} + \cdots + a_{S_{L-1}}^{(L-1)}\theta_{tS_{L-1}}^{(L-1)} \Big) \delta^{(L)}_t\\ &=\theta_{tx}^{(L-1)} \delta^{(L)}_t.\\ \end{aligned}\]

따라서,

\[\sum_{t=1}^{S_L} \frac{\partial z_t^{(L)}}{\partial a^{(L-1)}_{x}} \delta^{(L)}_t = \theta_{1x}^{(L-1)}\delta_1^{(L)}+\theta_{2x}^{(L-1)}\delta_2^{(L)} + \cdots + \theta_{S_{L}x}^{(L-1)}\delta_{S_{L}}^{(L)}.\]

$l=p$일 때 성립함을 가정하면,

\[\sum_{t=1}^{S_L} \frac{\partial z_t^{(L)}}{\partial a^{(p)}_{x}} \delta^{(L)}_t = \theta_{1x}^{(p)}\delta_1^{(p+1)}+\theta_{2x}^{(p)}\delta_2^{(p+1)} + \cdots + \theta_{S_{p+1}x}^{(p)}\delta_{S_{p+1}}^{(p+1)}.\]

다음과 같이 $l=p-1$ 일 때 성립함을 보일 수 있다.

\[\begin{aligned} \sum_{t=1}^{S_L} \frac{\partial z_t^{(L)}}{\partial a^{(p-1)}_{x}} \delta^{(L)}_t &= \sum_{t=1}^{S_L}\Big[ \frac{\partial a_1^{(p)}}{\partial a^{(p-1)}_{x}} \frac{\partial z_t^{(L)}}{\partial a^{(p)}_{1}}\delta^{(L)}_t \Big] + \sum_{t=1}^{S_L}\Big[ \frac{\partial a_2^{(p)}}{\partial a^{(p-1)}_{x}} \frac{\partial z_t^{(L)}}{\partial a^{(p)}_{2}}\delta^{(L)}_t \Big] + \cdots + \sum_{t=1}^{S_L}\Big[ \frac{\partial a_{S_p}^{(p)}}{\partial a^{(p-1)}_{x}} \frac{\partial z_t^{(L)}}{\partial a^{(p)}_{S_p}}\delta^{(L)}_t \Big] \\ &= \frac{\partial a_1^{(p)}}{\partial a^{(p-1)}_{x}} \Big[ \theta_{11}^{(p)}\delta_1^{(p+1)}+\theta_{21}^{(p)}\delta_2^{(p+1)} + \cdots + \theta_{S_{p+1}1}^{(p)}\delta_{S_{p+1}}^{(p+1)} \Big] + \\ &\phantom{000}\frac{\partial a_2^{(p)}}{\partial a^{(p-1)}_{x}} \Big[ \theta_{12}^{(p)}\delta_1^{(p+1)}+\theta_{22}^{(p)}\delta_2^{(p+1)} + \cdots + \theta_{S_{p+1}2}^{(p)}\delta_{S_{p+1}}^{(p+1)} \Big] + \\ &\phantom{000} \cdots + \frac{\partial a_{S_p}^{(p)}}{\partial a^{(p-1)}_{x}} \Big[ \theta_{1S_p}^{(p)}\delta_1^{(p+1)}+\theta_{2S_p}^{(p)}\delta_2^{(p+1)} + \cdots + \theta_{S_{p+1}S_p}^{(p)}\delta_{S_{p+1}}^{(p+1)} \Big] \\ &= \theta^{(p-1)}_{1x} g'(z_1^{(p)}) \Big[ \theta_{11}^{(p)}\delta_1^{(p+1)}+\theta_{21}^{(p)}\delta_2^{(p+1)} + \cdots + \theta_{S_{p+1}1}^{(p)}\delta_{S_{p+1}}^{(p+1)} \Big] + \\ &\phantom{000} \theta^{(p-1)}_{2x} g'(z_2^{(p)}) \Big[ \theta_{12}^{(p)}\delta_1^{(p+1)}+\theta_{22}^{(p)}\delta_2^{(p+1)} + \cdots + \theta_{S_{p+1}2}^{(p)}\delta_{S_{p+1}}^{(p+1)} \Big] + \\ &\phantom{000} \cdots + \theta^{(p-1)}_{S_px} g'(z_{S_p}^{(p)}) \Big[ \theta_{1S_p}^{(p)}\delta_1^{(p+1)}+\theta_{2S_p}^{(p)}\delta_2^{(p+1)} + \cdots + \theta_{S_{p+1}S_p}^{(p)}\delta_{S_{p+1}}^{(p+1)} \Big] \\ &= \theta_{1x}^{(p-1)}\delta_1^{(p)}+\theta_{2x}^{(p-1)}\delta_2^{(p)} + \cdots + \theta_{S_{p}x}^{(p-1)}\delta_{S_{p}}^{(p)}. \end{aligned}\]

• 0 Comments